为了实现纳米制造工艺的可控性,在纳米制造中对纳米结构的形貌参数进行快速、低成本、非破坏性地精确测量具有十分重要的意义。光学测量技术因其速度快、低成本、无接触、非破坏和易于在线集成等优点,近年来受到越来广泛的关注。光学测量技术可分为无模型测量技术和基于模型的测量技术。无模型测量技术如基于传统光学显微镜的测量技术,直接通过边缘识别的方式获得待测样品几何尺寸。这种“所见即所得”的测量技术由于受到衍射极限的影响,一般难以测量200 nm以下的结构。与之相比,基于模型的测量技术,并非直接通过边缘识别,而是首先对样品进行正向的光学特性建模,进而将模型生成数据与仪器测量数据进行比较,通过某种优化算法,最终反演出待测样品的信息。因这类基于模型的测量技术中引入了大量的数学计算,为突出这一特点,我们在国际上明确提出将这类测量称为“计算测量”。
(1) 计算测量基本概念
我们将计算测量定义为“对复杂测量过程进行建模计算并通过测量仪器在一定观测条件下获得观测数据,然后通过逆问题精确求解以获得待测参数的一种测量方法”。它包括待测参数、观测条件、观测数据、正向传递特性模型、测量结果等基本元素。在此基础上,课题组以基于穆勒矩阵椭偏仪的纳米结构测量为实例,针对计算测量中的一些科学问题与基础理论方法进行了系统的研究,验证了计算测量方法的可行性和有效性。
(2) 计算测量正向模型快速准确数值计算方法
在光学散射测量过程中,目前多采用严格耦合波分析方法来实现纳米结构散射场的建模求解。然而,该方法运算过程中通常都会涉及大量的本征值求解及密矩阵运算问题。特别地,当模型参数发生变化时需要反复进行正向建模计算,导致计算过程较为耗时。为此,我们将传统边界元法与减基法相结合以实现正向模型的快速准确计算。该方法以边界元法为基础,通过参数分离将边界积分方程的求解分解为与模型参数无关的离线计算和与模型参数相关的在线计算两部分,并将高维边界元解空间映射为低维解空间,从而大大减小求解边界积分方程的运算量。
(3) 计算测量待测参数快速鲁棒提取算法
目前,在计算测量中针对待测参数提取这一问题,传统的做法是通过迭代优化算法如GN (Gauss-Newton)法或LM (Levenberg-Marquardt)法来逐步最小化一个预先定义的LSQ(Least Square)评价函数,然而,这些传统的方法都对测量数据中的测量误差作了正态分布假设,真实的测量误差则要复杂的多。为了实现待测参数的鲁棒提取,我们提出了一种基于鲁棒统计学原理的纳米结构形貌重构新方法,该方法通过在传统的GN迭代法每一个迭代步中引入一个鲁棒修正回归步骤,来逐步抑制非正态分布测量误差对迭代结果的影响,从而极大提高了参数的提取准确度。
(4) 计算测量优化配置策略
在计算测量中,模型输入结构参数对输出光谱的灵敏度是影响待测纳米结构最终测量精确度的关键因素之一。由于在不同的入射波长、入射角、方位角等测量条件下,模型输出光谱对待测结构参数的灵敏度也不同。因此,我们提出了一种基于全局灵敏度分析的测量条件优化配置方法。对于正向模型,我们将其简单看成一个输入量包括测量配置(入射波长、入射角和方位角的组合)和纳米结构参数,输出量为光谱数据的非线性数学模型。通过同时变动所有的待测参数,利用基于方差的Sobol法和傅里叶幅度灵敏度检验扩展法计算出待测纳米结构参数的集总灵敏度系数,并结合各测量条件下的实际测量误差定义了不确定度指数作为测量条件优化配置的目标函数。其中,纳米结构参数的不确定指数越小,则该配置下对应待测参数的测量精确度越高。
(5) 计算测量的误差分析与不确定度评定方法
计算测量过程中的误差包括观测数据中随机噪声引起的随机误差,以及测量仪器和正向模型共同引起的系统误差。对于随机误差,可以将其看成随机变量,借助概率论与数理统计来研究。通过计算观测数据对待测参数的Hessian矩阵,可以求得待测参数的协方差矩阵,进而求得各个参数的方差以及参数之间的相关系数,据此可进一步评价测量结果的精确度以及参数之间的耦合性。对于系统误差,可以在逆问题求解过程中对正向传递特性函数在待测参数最优值及名义测量条件附近做一阶Taylor展开,通过一定的矩阵运算可以得到不同来源的系统误差对最终测量结果准确度的影响。
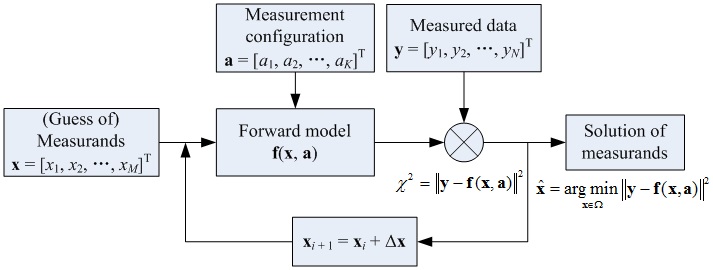
图1 计算测量概念与基本要素
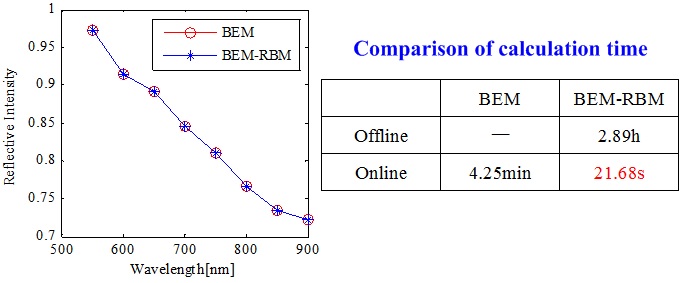
图2 BEM-RBM结合的方法与传统BEM方法之间计算精度和时间的对比
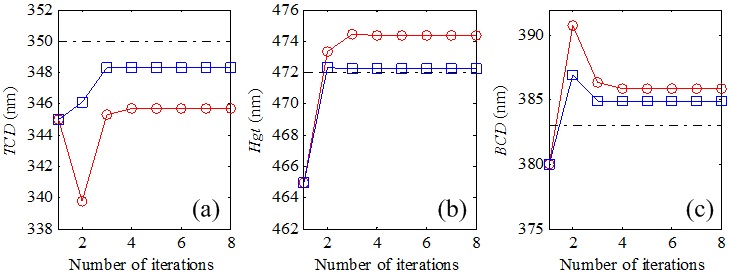
图3 基于GN算法(红色圆圈)和鲁棒优化算法(蓝色矩形)的参数迭代提取结果(虚线为SEM测量结果)
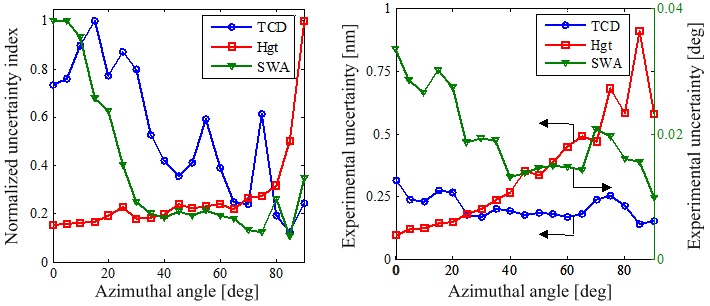
图4 基于不确定指数预测待测参数TCD,Hgt和SWA的最佳测量方位角分别85°,0°和85°,与实验得到的最佳方位角基本吻合。
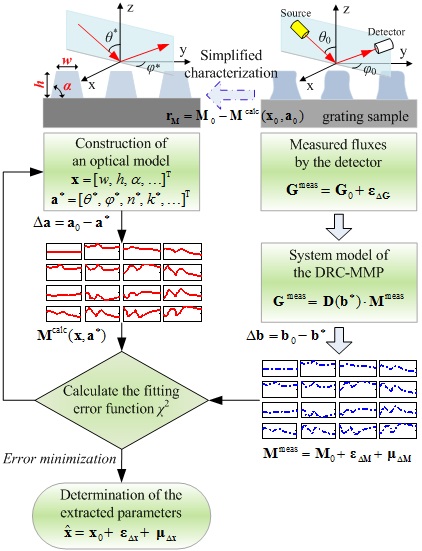
图5 基于穆勒矩阵椭偏仪的纳米结构测量中的误差传递流程图
代表性论文
J. L. Zhu, S. Y. Liu, X. G. Chen, C. W. Zhang, and H. Jiang, "Robust solution to the inverse problem in optical scatterometry," Opt. Express 22(18), 22031-22042 (2014). (URL, PDF)
Z. Q. Dong, S. Y. Liu, X. G. Chen, and C. W. Zhang, "Determination of an optimal measurement configuration in optical scatterometry using global sensitivity analysis," Thin Solid Films 562, 16-23 (2014). (URL, PDF)
X. G. Chen, S. Y. Liu, H. G. Gu, and C. W. Zhang, "Formulation of error propagation and estimation in grating reconstruction by a dual-rotating compensator Mueller matrix polarimeter," Thin Solid Films 571, 653-659 (2014). (URL, PDF)
刘世元,"计算测量问题与求解方法初探," 机械工程学报 50(4), 1-10 (2014). (URL, PDF)
S. Y. Liu, "Computational metrology for nanomanufacturing," Presented at the 6th International Symposium on Precision Mechanical Measurement (ISPMM), Guiyang, China, August 8-10, 2013, in Proc. SPIE 8916, 891606 (2013). (Invited speech) (URL, PDF)
X. G. Chen, S. Y. Liu, C. W. Zhang, and H. Jiang, "Improved measurement accuracy in optical scatterometry using correction-based library search," Appl. Opt. 52(27), 6727-6734 (2013). (URL, PDF)
X. G. Chen, S. Y. Liu, C. W. Zhang, and H. Jiang, "Measurement configuration optimization for accurate grating reconstruction by Mueller matrix polarimetry," J. Micro/Nanolith. MEMS MOEMS 12(3), 033013 (2013). (URL, PDF)
X. G. Chen, S. Y. Liu, C. W. Zhang, and J. L. Zhu, "Improved measurement accuracy in optical scatterometry using fitting error interpolation based library search," Measurement 46(8), 2638-2646 (2013). (URL, PDF)
J. L. Zhu, S. Y. Liu, C. W. Zhang, X. G. Chen, and Z. Q. Dong, "Identification and reconstruction of diffraction structures in optical scatterometry using support vector machine method," J. Micro/Nanolith. MEMS MOEMS 12(1), 013004 (2013). (URL, PDF)
S. Y. Liu, Y. Ma, X. G. Chen, and C. W. Zhang, "Estimation of the convergence order of rigorous coupled-wave analysis for binary gratings in optical critical dimension metrology," Opt. Eng. 51(8), 081504 (2012). (URL, PDF)