目前,工业界广泛使用193 nm波长的浸没式光刻机来制造关键尺寸远小于波长的集成电路芯片,制造过程相当于用粗大的刷子画细小的线条,已经远远超出了物理范畴上的极限分辨率。计算光刻技术使得这种“用大刷子画细线条”的制造变成可能,并且保证了大批量的制造,它已经成为了摩尔定律的主要推动力之一。计算光刻的原理是使用计算仿真的方法,将包含照明光源、掩模、投影物镜系统的成像系统和光刻胶曝光、刻蚀等工艺过程联系起来,然后通过数学的方法进行掩模图形分拆与校正、光源照明形状优化、投影物镜参数调节等方式增强分辨率。计算光刻的成功与否极大程度上取决于两大关键技术,即快速准确的正向光学成像建模与高效鲁棒的逆向光源掩模优化。针对两大关键技术,本研究组开展了一系列研究工作。
(1) 光刻光学成像快速计算方法
基于圆采样函数的成像系统核函数分解方法。将成像系统的四维交叉传递系数矩阵投影到圆采样函数空间得到投影系数矩阵,对该矩阵进行奇异值分解,分解的向量和圆采样函数结合得到系统的核函数。这种方法避免了直接对四维交叉传递系数矩阵进行奇异值分解,极大的减少了计算时间;而且,得到的核函数具有解析的形式,可以灵活设置不同的分辨率。
基于单个基本掩模的空间像快速计算方法。为提高光学临近校正过程中空间像的计算速度,根据单个基本掩模与系统的核函数,建立一个卷积表并提前存储起来,将集成电路中的多边形掩模表征成若干个平移后的基本掩模的叠加,通过查表得到整个掩模空间像。这种方法非常适合于光学临近校正里面的空间像计算。
(2) 基于卷积变量分离算法的矢量光刻成像建模快速算法
考虑多种工艺参数的光刻成像建模快速算法。提出一种基于卷积变量分离的新方法,在不牺牲计算精度的情况下,可以高效计算多工艺参数变化时的光刻成像。该方法从光刻成像第一性原理出发,推导出一种极为简练而优美的级数和表达形式,由一系列基函数及其加权系数组成。其中,加权系数只与工艺参数有关,但基函数涉及卷积计算,因而非常耗时。但基函数与工艺数无关,因此可以事先计算并存储起来。当工艺参数改变时,只需把加权系数与事先计算好的基函数相乘并求和,即可得到预期的光刻成像结果。该方法已成功应用于考虑离焦量分布的鲁棒逆光刻技术中,以及考虑波像差时的光刻成像高效建。
基于厚掩模传递函数高效表达的矢量成像快速算法。提出一种可以快速计算多入射角条件下厚掩模传递函数的方法,该方法可以用于快速的计算基于多入射角下厚掩模的矢量空间像。该方法推导出一种简练级数和表达形式,由一系列基函数及其加权系数组成。其中,加权系数只与入射角有关,但基函数有严格电磁波计算得到,因而非常耗时。但基函数与入射角度无关,因此可以事先计算并存储起来。当入射角改变时,只需把加权系数与事先计算好的基函数相乘并求和,即可得到预期的掩模近场分布。该方法已成功应用于不同入射角下厚掩模近场分布及矢量空间像的计算,显示了新方法的高效性能,同时希望该方法可以用于光学临近矫正技术和逆光刻计术中。
(3) 快速鲁棒的光源掩模逆向设计算法
基于多重网格的快速掩模设计方法。该方法首先依据表征掩模的网格格点尺寸大小对掩模进行分级,在粗网格上快速求解掩模,然后对在粗网格上求解得到的掩模进行插值传播到下一级较细网格上进行细化校正,最终实现了掩模的快速优化。这种方法比传统的单一格点优化方法快4倍。
掩模可制造性增强方法。提出了基于水平集的逆向掩模设计方法,将掩模表征成一个水平集函数,进而将掩模优化问题转化为水平集函数的优化,通过这种方法优化得到掩模图形复杂度低,轮廓光滑;提出了基于掩模滤波技术的掩模正则化方法,设计了一个掩模滤波器直接作用在掩模上,滤波器可以直接过滤掩模中孤岛、断线、灰度等信息,保证了在每次迭代过程中掩模的可制造性。
基于统计学原理的鲁棒的掩模优化策略。该方法考虑现实中工艺参数(比如离焦、曝光剂量)的概率分布,优化掩模相对于不同工艺分布下的平均效果。该方法提高了优化后掩模的鲁棒性,极大的增大了工艺窗口。
基于无导数优化方法的严格的光源优化方法。提出了一个新的光源图形表达方法,具有适中的参数变量,并且考虑了现实光源非负、有界等特性。根据这种表达方法,光源优化问题就转化为优化这些参数变量。将多参数的优化依次转化为一个较小区域内某单一参数的优化,并计算相应的最优值,从而优化全部参数。该方法不需要成像系统的解析表达式以及梯度信息,而且跟目标函数的形式无关,非常适合于严格成像模型下的光源优化。
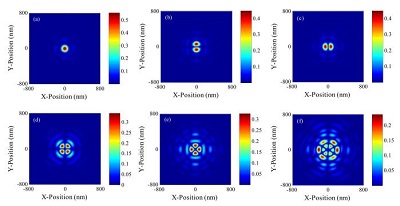
图1 基于圆采样函数分解得到的开始的6个核函数
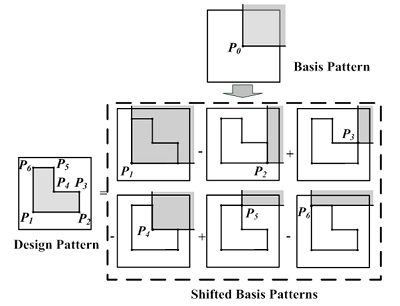
图2 基于单个基本掩模的掩模图形表达原理
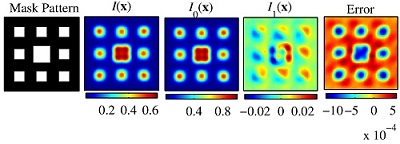
图3 考虑波像差时的光刻成像分离与高效建模计算结果
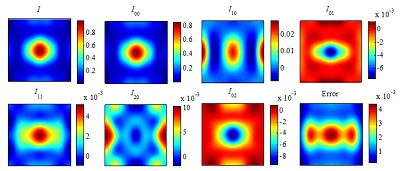
图4 基于多入射角下掩模传递函数的矢量空间像仿真结果
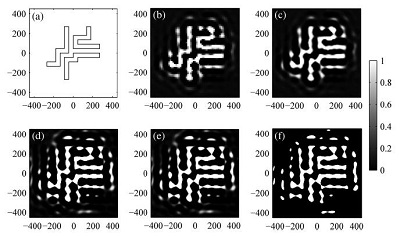
图5 基于多重网格的掩模优化结果。(a)目标图形。(b)在最粗网格优化得到的掩模。(c)由(a)插值到较粗网格。(d)在较粗网格优化得到的掩模。(e)由(d)插值到最密网格。(f)在最密网格得到的图形。
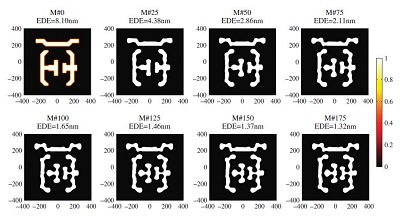
图6 采用掩模滤波方法在掩模优化过程中得到的中间掩模。
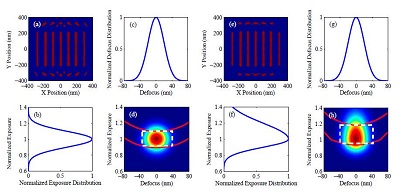
图7 不同工艺分布下优化得打的掩模和相应的工艺窗口。(a)在离焦分布(c)和曝光剂量分布(b)下得到的掩模,(d)是相应的工艺窗口。(e)在离焦分布(g)和曝光剂量分布(f)下得到的掩模,(h)是相应的工艺窗口。
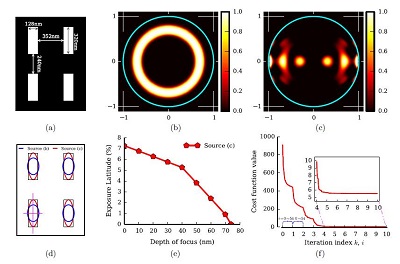
图8 基于无导数优化方法的光源优化。(a)bricks掩模,关键尺寸128nm/4=32 nm。(b)初始光源。(c)优化的光源。(d)光源(a)和(b)在硅片上成像的轮廓对比。(e)光源(b)工艺窗口;光源(a)无工艺窗口。(f)收敛曲线。
代表性论文
W. Lv, S. Y. Liu, X. F. Wu, and E. Y. Lam, "Illumination source optimization in optical lithography via derivative-free optimization," J. Opt. Soc. Am. A, 31(12), B19-B27(2014). (URL, PDF)
X. J. Zhou, C. W. Zhang, H. J. Jiang, H. Q. Wei, and S. Y. Liu, "Efficient representation of mask transmittance functions for vectorial lithography simulations," J. Opt. Soc. Am. A, 31(12), B10-B18 (2014). (URL, PDF)
W. Lv, E. Y. Lam, H. Q. Wei, and S. Y. Liu, "Cascadic multigrid algorithm for robust inverse mask synthesis in optical lithography," J. Micro/Nanolith. MEMS MOEMS 13(2), 023003 (2014). (URL, PDF)
S. Y. Liu, X. J. Zhou, W. Lv, S. Xu, and H. Q. Wei, "Convolution-variation separation method for efficient modeling of optical lithography," Opt. Lett. 38(13), 2168-2170 (2013). (URL, PDF)
W. Lv, Q. Xia, and S. Y. Liu, "Mask-filtering-based inverse lithography," J. Micro/Nanolith. MEMS MOEMS 12(4), 043003 (2013). (URL, PDF)
W. Lv, S. Y. Liu, Q. Xia, X. F. Wu, Y. Y. Shen, and E. Y. Lam, "Level-set-based inverse lithography for mask synthesis using the conjugate gradient and an optimal time step," J. Vac. Sci. Technol. B 31(4), 041605 (2013). (URL, PDF)
P. Gong, S. Y. Liu, W. Lv, and X. J. Zhou, "Fast aerial image simulations for partially coherent systems by transmission cross coefficient decomposition with analytical kernels," J. Vac. Sci. Technol. B 30(6), 06FG03 (2012). (URL, PDF)
S. Y. Liu, W. Liu, X. J. Zhou, and P. Gong, "Kernel-based parametric analytical model of source intensity distributions in lithographic tools," Appl. Opt. 51(10), 1479-1486 (2012). (URL, PDF)
S. Y. Liu, X. F. Wu, W. Liu, and C. W. Zhang, "Fast aerial image simulations using one basis mask pattern for optical proximity correction," J. Vac. Sci. Technol. B 29(6), 06FH03 (2011). (URL, PDF)