In order to achieve effective process control, fast, inexpensive, nondestructive, and reliable nanometer scale feature measurements are extremely useful in nanomanufacturing. Optics-based metrology tools, which have drawn more and more attention in semiconductor manufacturing because of their attractive advantages, such as low cost, non-contact, non-destruction, and high throughput, may be one of the best choices. Overall, optics-based metrology can be classified into two categories, namely the model-free and the model-based methods. Model-free metrology, such as the conventional optical microscopy, seems to be useless for nanoscale dimensional analysis due to the so-called diffraction limit. In contrast, model-based metrology, such as optical scatterometry, does not depend on images with well-defined edges and allows for the indirect determination of the geometrical parameters of the measuring targets from the measured signatures. Since this model-based metrology relies heavily on forward optical modeling and inverse parameter extraction, which are both computationally intensive, we term this metrology as computational metrology (CM). To the best of our knowledge, it is the first time we give this term similar to the case of computational lithography (CL), with emphasis on solving the mathematical problems.
(1) Fundamental concept of computational metrology
Computational metrology is defined as "a measurement method where a complicated measurement process is modeled as a forward problem and some measured data are obtained by a specific instrument under a certain measurement configuration, and then the measurands are precisely and accurately reconstructed by solving the corresponding inverse problem." The basic elements of computational metrology include the measurands, measurement configuration, forward model, measured data, and solution of measurands. We have investigated and verified some fundamental problems and solution methods in computational metrology by taking the Mueller matrix ellipsometry for nanostructure metrology as a case study.
(2) Fast and accurate numerical methods for forward modeling
The most commonly used method for the scattering field modeling of nanostructures (especially periodic nanostructures) is rigorous coupled-wave analysis (RCWA). However, the computational process of RCWA involves intensive calculations involving eigenvalue problems and dense matrices. Particularly, repeated computations of the forward model are inevitable when the modeling parameters change, and thereby leads to a time-consuming process. To realize fast and accurate forward modeling, we propose to combine the traditional boundary element method (BEM) with the reduced-basis method (RBM). In this combined method, the calculation of the boundary integral equation is divided into a parameter-independent offline process and a parameter-dependent online process. In addition, the high-dimensional solution space is mapped into a low-dimensional solution space, which significantly reduces the computational complexity.
(3) Fast and robust measurand reconstruction algorithms
Currently, the traditional method in computational metrology for parameter extraction uses gradient-based iterative algorithms such as the Gauss-Newton (GN) and Levenberg-Marquardt (LM), whose core is the iterative minimization of a pre-defined least square (LSQ) function. The LSQ function implies an assumption of the statistical property of measurement errors, namely, the assumption of zero mean with normal distribution. However, the actual statistical property of measurement errors is far more complex than the simple normal distribution. To realize a more robust parameter extraction, we propose to add a robust regression procedure at the end of each iteration of the GN algorithm to obtain a more accurate parameter departure vector, by which more accurate reconstructed results can be achieved.
(4) Measurement configuration optimization
In computational metrology, the sensitivity of the model inputs on the output has a significant impact on the precision of the reconstructed profile parameters beyond the quality of the measured signatures and depends on the selected measurement configuration (a combination of wavelengths, incidence and azimuthal angles). Thus, we propose to determine an optimal measurement configuration with the application of global sensitivity analysis (GSA). For each measurement configuration, we define called the uncertainty index to evaluate the impact of random noise in measured signatures on measurement precision by combining the corresponding noise level with the main effect defined in GSA. Experiments demonstrated that the lower the uncertainty index, the better the precision of the profile parameters.
(5) Error analysis and uncertainty estimation
In computation metrology, the errors can be generally categorized into random and systematic errors. The random errors are mainly induced by random noise in measured data, and can be studied by using probability and statistics. In detail, we first calculate the Hessian matrix of the measurands, and then obtain the variances and parameter correlation coefficients from the corresponding covariance matrix. Finally, the measurement precision and parameter correlation can be estimated. Systematic errors are induced by both the instrument and the forward model. First, we do a first order Taylor expansion of the forward model in the vicinity of the nominal measurement condition and the solution of measurands. Then, the impact of various systematic errors on the accuracy of final measurement results can be estimated by making some matrix computations.
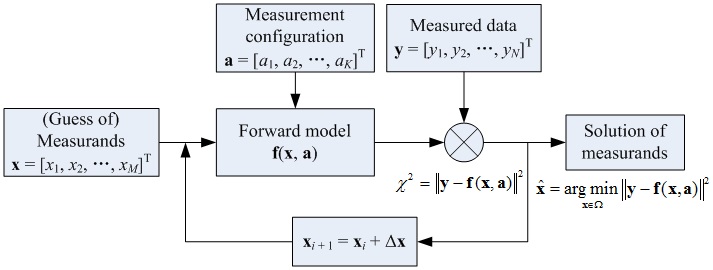
Fig. 1. Fundamental concept and basic elements of computational metrology
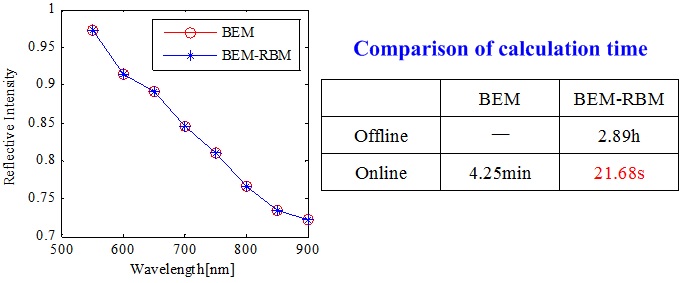
Fig. 2. The comparison of calculation accuracy and time between the conventional BEM and BEM-RBM combined method
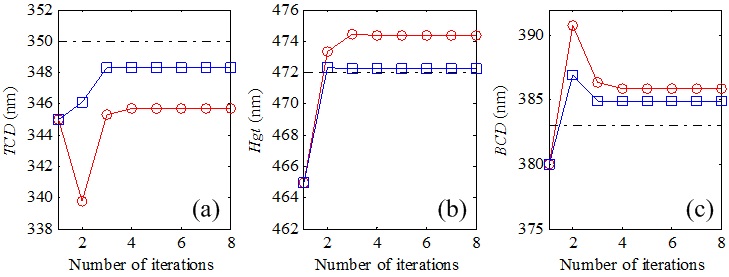
Fig. 3. The comparison of solutions of measurands obtained by the GN-based algorithm (with red circles) and proposed robust algorithm (with blue rectangles). The dash-dotted lines denote the results measured by SEM.
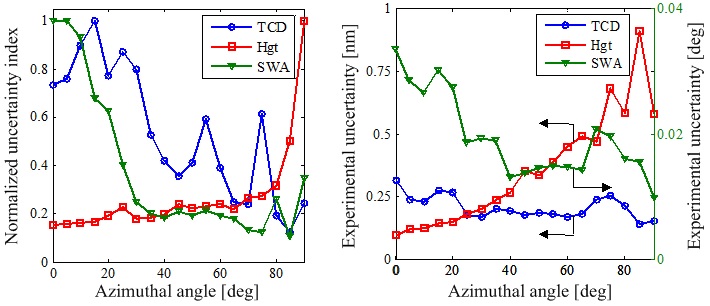
Fig. 4. The achieved optimal azimuthal angles for the measurands - TCD, Hgt, and SWA, are 85°, 0°and 85°, respectively, which are in reasonable agreement with the actually optimal azimuthal angles.
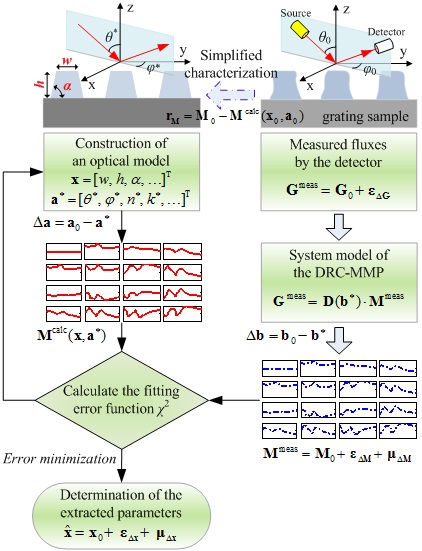
Fig. 5. Error propagation in nanostructure metrology using Mueller matrix ellipsometry
Secleted papers
J. L. Zhu, S. Y. Liu, X. G. Chen, C. W. Zhang, and H. Jiang, "Robust solution to the inverse problem in optical scatterometry," Opt. Express 22(18), 22031-22042 (2014). (URL, PDF)
Z. Q. Dong, S. Y. Liu, X. G. Chen, and C. W. Zhang, "Determination of an optimal measurement configuration in optical scatterometry using global sensitivity analysis," Thin Solid Films 562, 16-23 (2014). (URL, PDF)
X. G. Chen, S. Y. Liu, H. G. Gu, and C. W. Zhang, "Formulation of error propagation and estimation in grating reconstruction by a dual-rotating compensator Mueller matrix polarimeter," Thin Solid Films 571, 653-659 (2014). (URL, PDF)
S. Y. Liu, "Computational metrology: Problems and solution methods," J. Mech. Eng. 50(4), 1-10 (2014). (URL, PDF)
S. Y. Liu, "Computational metrology for nanomanufacturing," Presented at the 6th International Symposium on Precision Mechanical Measurement (ISPMM), Guiyang, China, August 8-10, 2013, in Proc. SPIE 8916, 891606 (2013). (Invited speech) (URL, PDF)
X. G. Chen, S. Y. Liu, C. W. Zhang, and H. Jiang, "Improved measurement accuracy in optical scatterometry using correction-based library search," Appl. Opt. 52(27), 6727-6734 (2013). (URL, PDF)
X. G. Chen, S. Y. Liu, C. W. Zhang, and H. Jiang, "Measurement configuration optimization for accurate grating reconstruction by Mueller matrix polarimetry," J. Micro/Nanolith. MEMS MOEMS 12(3), 033013 (2013). (URL, PDF)
X. G. Chen, S. Y. Liu, C. W. Zhang, and J. L. Zhu, "Improved measurement accuracy in optical scatterometry using fitting error interpolation based library search," Measurement 46(8), 2638-2646 (2013). (URL, PDF)
J. L. Zhu, S. Y. Liu, C. W. Zhang, X. G. Chen, and Z. Q. Dong, "Identification and reconstruction of diffraction structures in optical scatterometry using support vector machine method," J. Micro/Nanolith. MEMS MOEMS 12(1), 013004 (2013). (URL, PDF)
S. Y. Liu, Y. Ma, X. G. Chen, and C. W. Zhang, "Estimation of the convergence order of rigorous coupled-wave analysis for binary gratings in optical critical dimension metrology," Opt. Eng. 51(8), 081504 (2012). (URL, PDF)