193nm ArF immersion lithography is widely used in the semiconductor industry to manufacture integrated circuits whose critical dimensions are much smaller than the source wavelength. The manufacturing process is similar to creating thin lines with a broad brush, which is physically beyond the resolution limit. Computational lithography (CL) enables this process and guarantees high volume production as well. It has been a driving force of Moore's Law. Computational lithography models the lithography process, including the imaging system (illumination source, mask, and projection lens) and the manufacturing process (such as exposing and etching), and mathematically performs mask division and correction, source optimization, and lens aberrations adjustments to enhance the resolution. The success of computational lithography relies heavily on two main procedures involved, namely, the fast and accurate forward optical imaging simulation and the fast and robust inverse source mask optimization strategy. We have carried out a series investigations to address these issues.
(1) Fast and accurate forward optical imaging simulations
Fast optical image simulation by transmission cross-coefficient decomposition with analytical kernels. Optical image simulation is one of the key parts in a model-based optical proximity correction (OPC) technique. To improve its computational efficiency, we propose a fast simulation method by decomposing the transmission cross-coefficient (TCC) into analytical kernels. The TCC matrix is projected onto a function space whose basis consists of analytical circle-sampling functions (CSFs) and is then converted into a much smaller projected matrix. By performing singular value decomposition (SVD) to the projected matrix, its eigenvectors, together with the CSFs, are used to generate a set of analytical kernels. This method avoids the need to directly perform SVD to the large TCC matrix, making it much more runtime efficient. Furthermore, the grid size of the kernels can be flexibly set to any desired value in optical image simulations.
Fast optical image simulation using one basis mask pattern. We propose an optical image simulation method by using one basis mask pattern to generate a lookup table, where the convolutions of the basis pattern with the kernels are pre-calculated and stored. A rectilinear polygon mask pattern used in integrated circuit layouts can be decomposed into several shifted basis patterns. Its convolutions with kernels for use in optical image calculation can then be quickly obtained from the pre-calculated lookup table by applying the translation-invariant property of two-dimensional convolution. Simulations conducted by using the proposed approach have demonstrated superior quality in the fields of optical image calculation and OPC.
(2) Vector imaging simulations using the convolution-variation separation method
Efficient optical imaging simulation with process variations. We propose a new method called convolution-variation separation (CVS) to enable efficient optical imaging calculations without sacrificing accuracy when simulating images for a wide range of process variations. The CVS method is derived from first principles using a series expansion, which consists of a set of predetermined basis functions weighted by a set of predetermined expansion coefficients. The basis functions are independent of the process variations and thus may be computed and stored in advance, while the expansion coefficients depend only on the process variations. Optical image simulations for defocus and aberration variations with applications in robust inverse lithography technology and lens aberration metrology have demonstrated the main concept and advantage of the CVS method.
Vector imaging simulation based on efficient representation of mask transmittance function. We propose a generalized method to efficiently represent the incident-angle-dependent mask transmittance function (MTF) of a thick mask. This method expands the MTF into a series expansion, which consists of a set of predetermined basis functions weighted by a set of predetermined expansion coefficients. The predetermined basis functions are independent of the incident angles and thus may be computed offline and stored, while the expansion coefficients depend only on the incident angles and can be rapidly calculated online. Near field and optical image simulations of thick masks have demonstrated the excellent accuracy and superior speed performance of the proposed method. We believe this work will present a new perspective aimed at significantly improving the speed of thick mask simulations without serious loss of accuracy, which has great potential for applications in optical approximation correction (OPC) and inverse lithography technology (ILT).
(3) Fast and robust inverse source mask optimization algorithms
Cascadic multigrid algorithm for fast inverse mask synthesis. We propose a cascadic multigrid (CMG) algorithm for fast inverse mask synthesis, which starts from a relatively coarse mask grid and refines it iteratively in stages, so as to achieve a significant increase in speed without compromising numerical accuracy. As a result, our algorithm achieves more than four times the increase in speed over conventional methods that synthesize a mask on a fixed fine grid.
Mask manufacturability enhancement methods. We propose a level-set method to solve the inverse mask synthesis problem where the boundary of the mask pattern is iteratively evolved instead of the mask itself. It results in a smooth mask contour. In addition, we propose a new regularization framework for inverse lithography that regularizes masks directly by applying a mask filtering technique to improve computational efficiency and to enhance mask manufacturability. This technique is different from the conventional regularization method that regularizes a mask by incorporating various penalty functions to the cost function.
Statistical strategy for robust inverse mask synthesis. As critical dimensions shrinks, the pattern density of integrated circuits becomes much denser, and lithographic process variations become more pronounced. In order to synthesize masks that are robust to process variations, the average wafer performance with respect to process fluctuations is optimized. This approach explicitly takes into account process variations. Furthermore, we investigate the impacts of arbitrary statistical distribution of process variations on the synthesized mask patterns.
Derivative-free optimization for source optimization under a rigorous simulation model. We perform source optimization (SO) in optical lithography under a rigorous simulation model which considers critical effects, such as the vector nature of light and mask topography. We propose a new source pattern representation method, which has moderate parameter variations but remains complete in the solution space. Then, we develop a derivative-free optimization (DFO) method to optimize these parameters under a rigorous simulation model. Unlike gradient-based techniques, DFO methods do not require a closed-form formulation of the model and are independent of the form of cost function.
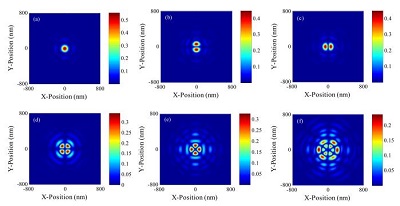
Fig. 1. First six kernels derived by the proposed TCC decomposition method.
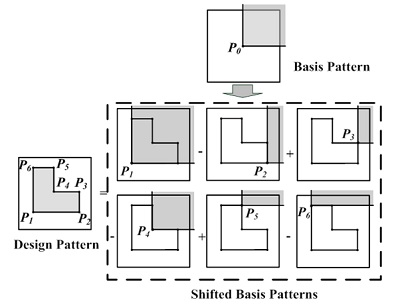
Fig. 2. Decomposition of any rectilinear polygon mask pattern into the sum of several shifted basis patterns according to their contributions.
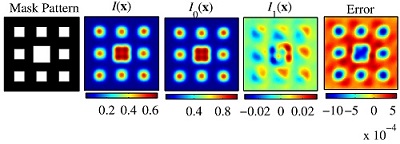
Fig. 3. Separation and efficient simulation of image intensity under lens aberrations.
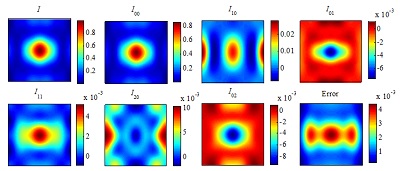
Fig. 4. Simulation results of the optical image intensity and its decomposition into different terms by using the method of incident-angle-dependent mask transmittance function (MTF).
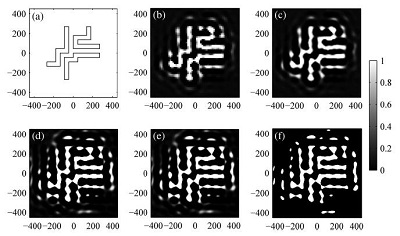
Fig. 5. Simulation results of the cascadic multigrid algorithm. (a) Desired pattern. (b) The synthesized mask pattern on the coarsest space. (c) The interpolated mask pattern of (b) to the less coarse space. (d) The synthesized mask pattern on the less coarse space. (e) The interpolated mask of (d) to the finest space. (f) The synthesized mask pattern on the finest space.
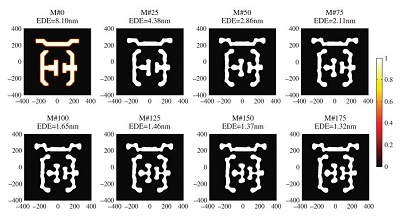
Fig. 6. Some intermediate results obtained in the iteration process using the mask filtering technique.
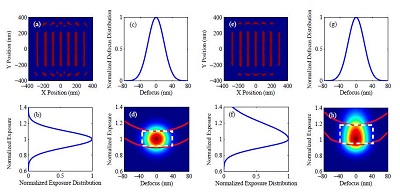
Fig. 7. Simulation results under different process distribution. (a) The synthesized mask pattern under the exposure distribution (b) and defocus distribution (c), (d) is its E-D window. (e) The synthesized mask pattern under the exposure distribution (f) and defocus distribution (g), (h) is its E-D window.
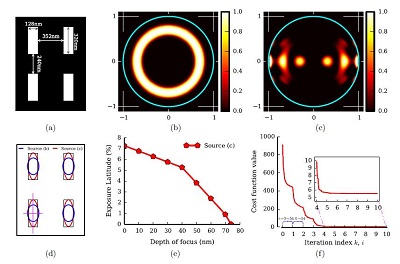
Fig. 8. Simulation results for a brick array pattern using the derivative-free optimization method. (a) Regular brick array. (b) Initial source. (c) The optimized source. (d) The contour comparison between the annular source (b) and the optimized source (c) on the wafer side. (e)The process latitude of the optimized source (c). Process latitude is unavailable with the annular source (b). (f) Convergence history.