With ever decreasing feature sizes, the impact of lens aberration has become increasingly important for imaging quality control of projection lithographic tools. The imaging optics configuration in lithographic tools is typically a partially coherent system characterized by the intensity distribution of the source and the pupil function of the projection lens. Imaging properties of such partially coherent systems have to be described using a bilinear model, which leads to time-consuming calculations and difficulties in comprehension, especially in the case when wavefront aberration is involved. Therefore, we have developed several novel methods for in situ measurement of lens aberrations up to the 37th (or even higher-order) Zernike coefficient in lithographic tools with partially coherent illumination.
(1) Analytical sensitivity functions for in-situ aberration measurement
By simplifying the theoretical derivation of optical imaging under partial coherent illumination, we propose two linear models in a compact expression with two matrices, and then used to determine the Zernike coefficients of odd aberration and even aberration, respectively. This technique has been extended with generalized formulations suitable for arbitrarily shaped illumination sources by further derivation of the analytical aberration sensitivities. The technique requires the acquisition and analysis of optical image intensities of a set of 36 binary gratings with different pitches and orientations. It is fully expected that this technique will be simple to implement and will provide a useful practical means for the in-line monitoring of imaging quality of lithographic tools under partial coherent illumination.
(2) Single-image method for direct aberration retrieval
Recently, we propose a method for retrieving small lens aberrations in partially coherent imaging systems, which only requires measuring one single defocused image of intensity. By deriving a linear theory of imaging systems, we obtain a generalized formulation of aberration sensitivity in a matrix form, which provides a set of analytic kernels that relate directly the measured intensity distribution to the unknown Zernike coefficients. Sensitivity analysis is performed and test patterns are optimized to ensure well-posedness of the inverse problem.
(3) In-situ aberration measurement using an efficient quadratic aberration model
In considering the case where the aberrations are relatively large, a rapid calculation of the quadratic or even higher order aberration model is required. We propose a fast algorithm by introducing a generalized operator called cross triple correlation (CTC). By decomposition of the transmission cross coefficient (TCC) into CTCs, the Zernike aberration-induced intensities in the quadratic aberration model can be quickly calculated and clearly separated from each other. Based on the proposed algorithm, we develop a method for in-situ aberration measurement based on the quadratic aberration model, which represents the bilinear relationship between the optical image intensity and the Zernike coefficients. The iterative algorithm is adopted to extract the Zernike coefficients from the through-focus optical images of a specially designed mask pattern. The simulation work has validated the theoretical derivation and confirms that such a method yields a superior quality of wavefront estimates, particularly for the case when the aberrations are relatively large.
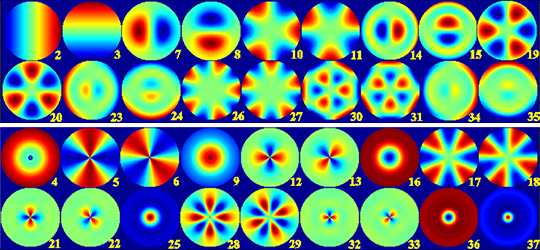
Fig. 1. Characterization of analytical kernels for measuring odd and even aberrations under a smooth conventional illumination.
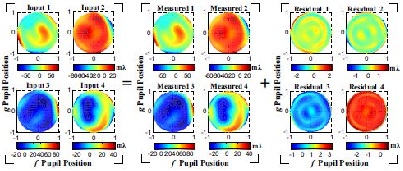
Fig. 2. Comparison between the input and measured aberrated wavefronts under the smooth quadrupole illumination.
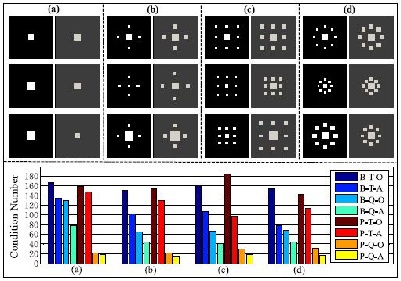
Fig. 3. Optimization results of some object patterns for single-image method, with (a) to (d) as four kinds of object patterns.
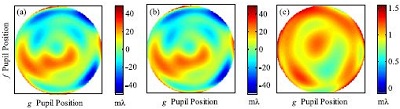
Fig. 4. Aberration retrieval results. (a) Unknown aberration, (b) retrieved aberration, and (c) wavefront error.
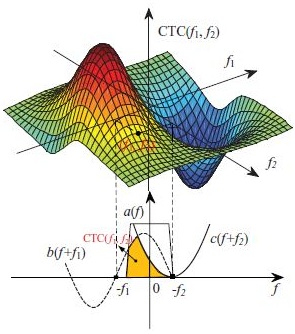
Fig. 5. Representation of the mathematical meaning of CTC
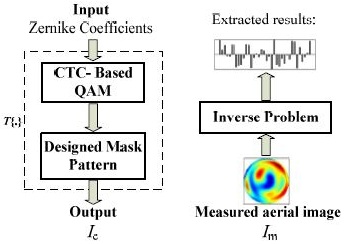
Fig. 6. Forward modeling and inverse problem for aberration measurement.
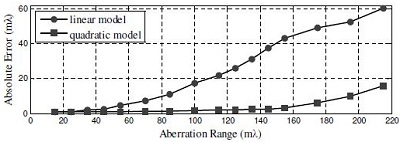
Fig. 7. Measurement accuracy by using the proposed quadratic model and the simplified linear model
Selected papers
S. Xu, C. W. Zhang, H. Q. Wei, and S. Y. Liu, "A single-image method of aberration retrieval for imaging systems under partially coherent illumination," J. Opt. 16(7), 072001 (2014). (URL, PDF)
S. Y. Liu, X. J. Zhou, W. Lv, S. Xu, and H. Q. Wei, "Convolution-variation separation method for efficient modeling of optical lithography," Opt. Lett. 38(13), 2168-2170 (2013). (URL, PDF)
S. Y. Liu, S. Xu, X. F. Wu, and W. Liu, "Iterative method for in situ measurement of lens aberrations in lithographic tools using CTC-based quadratic aberration model," Opt. Express 20(13), 14272-14283 (2012). (URL, PDF)
S. Y. Liu, W. Liu, and T. T. Zhou, "Fast algorithm for quadratic aberration model in optical lithography based on cross triple correlation," J. Micro/Nanolith. MEMS MOEMS 10(2), 023007 (2011). (URL, PDF)
S. Y. Liu, W. Liu, and X. F. Wu, "Fast evaluation of aberration-induced intensity distribution in partially coherent imaging systems by cross triple correlation," Chin. Phys. Lett. 28(10), 104212 (2011). (URL, PDF)
W. Liu, S. Y. Liu, T. L. Shi, and Z. R. Tang, "Generalized formulations for aerial image based lens aberration metrology in lithographic tools with arbitrarily shaped illumination sources," Opt. Express 18(19), 20096-20104 (2010). (URL, PDF)
W. Liu, S. Y. Liu, T. T. Zhou, and L. J. Wang, "Aerial image based technique for measurement of lens aberrations up to 37th Zernike coefficient in lithographic tools under partial coherent illumination," Opt. Express 17(21), 19278-19291 (2009). (URL, PDF)